Me sacaron tajadas y tajadas…
septiembre 2, 2008
¿Es posible asignar a cada ![x \in [0,1]](https://s0.wp.com/latex.php?latex=x+%5Cin+%5B0%2C1%5D&bg=ffffff&fg=555555&s=0&c=20201002)
![x, y \in [0,1]](https://s0.wp.com/latex.php?latex=x%2C+y+%5Cin+%5B0%2C1%5D&bg=ffffff&fg=555555&s=0&c=20201002)
- Comentarios
- Rebloguear
-
Suscribirse
Suscrito
¿Ya tienes una cuenta de WordPress.com? Inicia sesión.
"Estoy en esa estapa de la vida en la que te comés un alfajor y te preguntás si habrá alguna forma de incluir ese hecho en tu tesis" Annonymus
¿Es posible asignar a cada
Seminario de Problemas 
Asumiendo la Hipótesis del Continuo, y a menos de error, es fácil armar los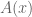
por inducción (!) ¿Se puede hacer menos ridículamente?
Aparentemente no, según un teorema de Sierpinski
(ver http://en.wikipedia.org/wiki/Freiling%27s_axiom_of_symmetry)
Es interesante leer los argumentos de Freiling en contra de la suposición del problema (y por tanto en contra de la HC) pero aunque es un análisis más bien heurístico, no sé si habría que descartarlo tan rápidamente…creo que el mismo Gödel estaba convencido de que el hecho de que HC sea independiente en ZF no hablaba muy bien de ZF y que por ahí habría que buscar algún otro sistema en donde no resulte independiente (de todos modos creo que él esperaba que fuera cierta). Pero parece que hay muchos que piensan que los axiomas tienen que construirse en base a la intuición, y que cuando un axioma es independiente, la decisión de agregar al axioma o a su negación debería hacerse por cuestiones intuitivas más que por lo que aporte a la teoría en sí…Yo no sé si estoy tan de acuerdo con eso…¿qué opinan?
Los axiomas los elegimos de acuerdo a lo que nos permiten probar.
El ejemplo canónico de esa visión se aprecia en un comentario de Hilbert después de escuchar a L. E. J. Brouwer dar una charla sobre su intuicionismo:
«With your methods most of the results of modern mathematics would have to be abandoned, and to me the important thing is not to get fewer results but to get more results.»
Diría que con HC sucede que nadie encontró (¿todavía?) algo tan eminentemente útil que requiera de HC para ser probado y que decida a las masas por adoptar a HC, ni nada suficientemente molesto que sea consecuencia de HC como para que uno quiera negar HC. Así, la cuestión parece siempre terminar por decidirse de acuerdo a las intuiciones personales, más allá de la razón. La enorme cantidad de enunciados equivalentes a HC que Sierpiński enumera en su librito Hypothèse du Continu son prácticamente irrelevantes para todo aquél que no esté haciendo teoría de conjuntos.
Un ejemplo de la situación contraria: la inducción transfinita. La base intuitiva se hace más pobre en cuanto uno considera ordinales más y más grandes, pero sirve para probar cosas como la consistencia de la aritmética de Peano (alcanza con poder hacer inducción hasta
, de hecho) y a todos más o menos nos da algo de tranquilidad que los axiomas de Peano sean consistentes. Así que aunque ni nuestros afirmaciones ni nuestras pruebas requieran de inducciones mucho más alla de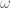 
, tenemos buenas razones para preferir sistemas axiomáticos en los que la prueba de Gentzen funcione.
Con el axioma de elección C pasa que uno logra probar con él cosas del estilo de Banach-Tarski, que nos marea a todos, pero al mismo tiempo nos asegura la existencia de ideales maximales en anillos conmutativos, o la compacidad débil-* de la bola unidad de nuestros espacios funcionales favoritos. En un ataque de pragmatismo—más o menos consciente—decidimos entonces quedarnos con C y convivir con algún que otro enunciado incómodo. Es más. no es difícil dar justificaciones para esa conviviencia: por ejemplo, aceptar que nuestra intuición inicial directamente no se aplica a conjuntos infinitos grandes.