En busca de la medida perdida

julio 9, 2008

Dado un conjunto simetrico respecto del origen y convexo $C\subset \mathbb{R}^2$ quiero demostrar que existe una medida $\mu$ con soporte en el convexo tal que la medida de cualesquiera dos franjas paralelas del mismo ancho sea la misma.

Nota: Por franja entiendase la region del convexo $C$ contenida entre dos rectas paralelas que intersecan al convexo. El ancho de una franja es la distancia entre ambas rectas.

Para el caso del circulo hay una construccion bastante linda. Tomen el circulo y piensenlo como el borde (plano) de una semiesfera. Ahora, a cada punto del circulo lo pueden proyectar a la semiesfera (en direccion perpendicular a la del plano del circulo). Tenemos asi una biyeccion entre el circulo y el casquete de la semiesfera. La medida buscada es la que resulta de traer para abajo la medida de la superficie de la semiesfera.

(perdon…… que mal que escribi lo anterior, cuando este con mas ganas lo escribo mejor).

Para el caso general, y quizas hay muchas condiciones de las que puse que estan de mas, mi idea es construir la densidad de esa medida (que tambien estara soportada en el convexo). Lo que tenemos es que las integrales de la funcion sobre las rectas que intersecan al convexo solo depende de su direccion. De ahi deberia salir usando la Transformada de Radon, lo que se tiene es que la transformada de Radon es ${\hat{r}}(\alpha, t)=\frac{1}{w(\alpha)} \chi_{-w(\alpha),w(\alpha)}(t)$ , donde $w(\alpha)$ es la mitad del ancho del convexo en la direccion $\alpha$ y $(\alpha, t)$ es la recta con direccion $\alpha$ a distancia $t$ del origen.

El problema con todo esto es que no se si para invertir la transformada de Radon hay que pedirle hipotesis de continuidad o que, y pero aun, cuando trate de hacer la cuenta con la formulita de la wikipedia las integrales me explotaron (aunque esto muy probablemente se debe a mi incapacidad de calcular integrales).

Otra cosa que me molesta, es pareciera ser que la densidad tiene que irse a infinito en el borde del convexo lo que la hace no ser una funcion muy linda.

Cualquier aporte sera bienvenido, ya sea via la transformada de Radon o via alguna construccion «a lo Marcos» de la medida.

Por ultimo les dejo el problema que motivo todo esto y su generalizacion (de la cual todavia no conozco ninguna solucion (y se que por un tiempo estuvo abierto (aunque el paper mas nuevo al respecto que vi creo que era del 60 mas o menos (y eso fue hace 3 o 4 años))).

Plank problem: Probar que si se cubre un circulo de radio ${1\over 2}$ con varias franjas entonces los anchos de todas las franjas suman al menos $1$ .

Plank problem mas fuerte: Probar que dado un convexo cubierto por varias franjas, los anchos relativos de las franjas suman al menos $1$ .

Nota: El ancho relativo de una franja es su ancho dividido el ancho del convexo en esa direccion.

Posted by charlydif

Filed in Uncategorized

5 Comments »

5 respuestas to “En busca de la medida perdida”

Julian Fernandez Bonder said
julio 9, 2008 at 11:16 pm
Carlos (y otros que les gusta la teoria de la medida). Perdon que aproveche esto para hacer un poco de propaganda, pero queria recomendarles el curso «El problema de transporte de masa» que va a dar Julio Rossi el 2do cuat.

El tema es muy interesante con muchos vinculos fundamentalmente entre teoria geometrica de la medida y ecuaciones diferenciales. Ademas de que Julio es uno de los mejores matematicos del departamento (y gran amigo).

Para chusmear un poco de que se trata el asunto, pueden ver http://math.berkeley.edu/~evans/Monge-Kantorovich.survey.pdf

Saludos

Responder
julianhaddad said
julio 11, 2008 at 9:30 am
Este problema se reduce al de la tomografía computada. Sabés la integral de la función restringida a las rectas. Alguien me había contado que podés recuperar la función sabiendo las integrales de todas las rectas a catorce direcciones distintas.

Responder
Julian said
julio 11, 2008 at 1:52 pm
Finalmente mi propaganda fue esteril. Julio no va a dar la materia este cuat.
Saludos

Responder
Grin Without a Cat said
julio 11, 2008 at 5:16 pm
FWIW, la medida para el caso del disco tiene en realidad densidad $\frac{1}{\sqrt{1-r^2}}$ , que es casi la que indica Carlos.

Como el problema se lleva bien con los cambios afines de coordenadas, además, de esa fórmula uno obtiene una fórmula explícita para elipses 😉

¿Alguien puede encontrar la densidad para un triángulo? (Otra vez, por simetría afín, basta hacerlo para un triángulo)

Responder
Grin Without a Cat said
julio 24, 2008 at 11:13 pm
Viajando hacia casa en colectivo caí en cuenta de que (creo) no necesariamente la densidad explota en los bordes: su valor en un punto depende de alguna manera misteriosa de cuántas—en proporción—secciones cortas pasan por el punto. Por ejemplo, cerca de los puntos medios de los lados de un rectángulo no hay mucha razón por la cual la densidad sea grande, ya que todas las secciones del rectángulo que pasan por puntos cercanos a ese son considerablemente largas.

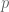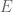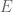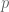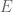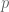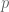Si el borde del convexo $K$ es ‘suficientemente’ chato (por ejemplo, si para cada punto $p$ del borde $K$ hay una elipse $E$ (llena y cerrada) tal que (i) $E$ está totalmente contenida en $K$ , (ii) su borde pasa por $p$ y (iii) la tangente a $E$ por $p$ es una recta soporte de $K$ en $p$ (¿esta última condición es consecuencia de las otras dos?) (esta condición excluye polígonos, por ejemplo))) entonces uno podría conujeturar que la densidad de Carlos tiene medida total finita…

Una cuenta que pude hacer en el colectivo a pesar de sus saltos es que la densidad, en el caso del disco, está dada precisamente por la fórmula

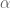$\delta(p)=\int_{\alpha}\frac{\mathrm d\alpha}{\ell_p(\alpha)^2}$

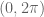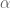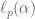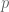donde $\alpha$ recorre $(0 , 2 \pi)$ , $\mathrm d\alpha$ es la medida usual, y para cada $p\in \mathrm{int}(K)$ y cada $\alpha$ , $\ell_p(\alpha)$ la longitud del segmento intersección de $K$ y la recta por $p$ que forma el ángulo 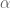$\alpha$ con el eje $x$ .

¿Hay alguna fórmula por el estilo para otro $K$ ?

Responder