La sombra de una duda…
May 12, 2008
Más sencillo imposible…
Sean y
cuerpos, tales que existen
, y
morfismos (en particular son inyectivos). ¿Es cierto entonces que los cuerpos son isomorfos?
"Estoy en esa estapa de la vida en la que te comés un alfajor y te preguntás si habrá alguna forma de incluir ese hecho en tu tesis" Annonymus
Más sencillo imposible…
Sean y
cuerpos, tales que existen
, y
morfismos (en particular son inyectivos). ¿Es cierto entonces que los cuerpos son isomorfos?
Si son non-numerables y algebraicamente cerrados, sí: la culpa es de los teoremas de Steinitz y de Cantor-Bernstein juntos.
Si son finitos tmb, pq tienen la misma cantidad de elementos y todos los cuerpos de igual cardinal son isomorfos.
Pablo, esta es una de las mejores preguntas del año!
No se lo que es el teorema de Steinitz.
Estaba bastante convencido que tenia una demostracion para el caso en que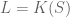 con
con  un conjunto de variables algebraicamente independientes pero cuando lo pense mejor me di cuenta que podia no andar.
un conjunto de variables algebraicamente independientes pero cuando lo pense mejor me di cuenta que podia no andar.
Creo que la mejor expresion del inconveniente es el siguiente ejemplo:
Si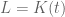 (con
(con 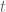 trascendente sobre
trascendente sobre  ) entonces es facil ver que hay morfimos en ambas direcciones pero tengo la impresion que no son isomorfos.
) entonces es facil ver que hay morfimos en ambas direcciones pero tengo la impresion que no son isomorfos.
Dado decimos que
decimos que  es «terriblemente trascendente» si existe un subcuerpo
es «terriblemente trascendente» si existe un subcuerpo  tal que
tal que  es tracendente sobre
es tracendente sobre 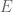 y
y  .
.
¿Tiene el antes definido elementos «terriblemente trascendentes»?
antes definido elementos «terriblemente trascendentes»?
No estoy seguro pero si creo que tambien hay problemas.
creo que tambien hay problemas.
En caso de ser falso el contraejemplo creo que me ayudaria a demostrar que la pregunta es cierta cuando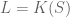 .
.
PD: ¿El teorema de Steinitz es que existe tal que
tal que  es algebraica?
es algebraica?
El teorema de Steinitz dice que dos cuerpos algebraicamente cerrados no numerables de la misma caracterśtica y el mismo cardinal son isomorfos. El lema de Cantor-Bernstein, que si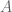 y
y 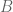 son conjuntos para los que hay inyecciones
son conjuntos para los que hay inyecciones  y
y 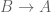 , entonces
, entonces 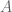 y
y 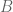 tienen el mismo cardinal. Juntando las dos cosas, uno obtiene el caso que mencioné, Es igual, entonces, que el caso finito, que observó phi, salvo que uno tiene que reemplazar el teorema de Steinitz por el de Galois, aquel que dice que dos cuerpos finitos equipotentes son isomorfos.
tienen el mismo cardinal. Juntando las dos cosas, uno obtiene el caso que mencioné, Es igual, entonces, que el caso finito, que observó phi, salvo que uno tiene que reemplazar el teorema de Steinitz por el de Galois, aquel que dice que dos cuerpos finitos equipotentes son isomorfos.
Dada una extensión , siempre existe
, siempre existe  tal que
tal que  es algebraica. Basta tomar un subconjunto
es algebraica. Basta tomar un subconjunto  de
de  maximal con respecto a la propiedad de ser algebraicamente independiente.
maximal con respecto a la propiedad de ser algebraicamente independiente.
A primera vista aprecía tan simple… en fin, qué bueno que haya sacado tanto jugo. Le debo unas buenas gracias a la alumna que nos preguntó esto en álgebra II. Lo más loco es que la pregunta salió a raíz de un ejercicio en el que los cuerpos eran finitos. Si la piba hubiera sabido un poco MAS de teoría de cuerpos, jamás hubiera hecho la pregunta…
I Love this sutff!
EDIT: Otro granito de arena. Si alguno es de dimensión finita sobre el cuerpo de base, también es cierto (los morfismos también son de espacios vectoriales sobre el cuerpo de base, y por lo tantos ambos tienen la misma dimensión. Esto implica que cada morfismo es biyectivo).
[…] 14, 2008 Con respecto a esta pregunta […]
PD: obvio que estaria bueno que opinen.
Una no-demostracion:
La primera vez que lei el mail de Mariano, yo entendi que decia usar eso de que si tenes una inyeccion de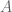 en
en 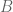 y una de
y una de 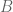 en
en 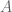 entonces hay una biyeccion que es en un pedazo de
entonces hay una biyeccion que es en un pedazo de 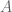 la funcion
la funcion 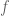 y en el restante la inversa de
y en el restante la inversa de  .
.
Si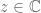 y
y  , sea
, sea 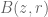 el disco abierto en
el disco abierto en 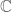 centrado en
centrado en  y de radio
y de radio  . Sean
. Sean  ,
,  y
y  , de manera que
, de manera que  . Para cada
. Para cada  , sea
, sea 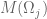 el cuerpo de las funciones meromorfas en
el cuerpo de las funciones meromorfas en 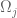 . Las inclusiones inducen aplicaciones
. Las inclusiones inducen aplicaciones 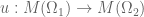 y
y  por restricción, que son morfismos de cuerpos. Como
por restricción, que son morfismos de cuerpos. Como 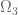 se obtiene de
se obtiene de  vía una homotecia, es claro que hay un isomorfimo de cuerpos
vía una homotecia, es claro que hay un isomorfimo de cuerpos 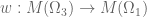 .
.
Pongamos y
y  y consideremos los morfismos
y consideremos los morfismos 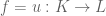 y
y 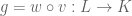 . Estamos en la situación del problema.
. Estamos en la situación del problema.
Ahora bien, en [Serbetçi,Ayhan; Özkin, I. Kaya: Meromorphic function fields on subsets of open Riemann surfaces. An. Stiint. Univ. Al. I. Cuza Iasi Sect. I a Mat. 39 (1993), no. 3, 259-265] se prueba que si dos superficies de Riemann no compactas tienen cuerpos de funciones meromorfas isomorfos (en tanto cuerpos abstractos) entonces o bien son holomórfamente equivalentes o bien son anti-holomórfamente equivalentes. En particular, en cualquiera de los dos casos, las superficies de Riemann son homeomorfas.
[Sigue…]
Pero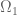 y
y  no son homeomorfas,
no son homeomorfas, .
.
porque el primero es simplemente conexo, mientras que el segundo
no lo es. Luego
PS: ¿Cómo editan los comentarios? La falta de una función de preview
me mata 😦
El teorema de Iss’sa (cf. Reinhold Remmert, Classical Topics in Complex Function theory, un librazo) afirma que todo morfismo es inducido por una función holomorfa
es inducido por una función holomorfa 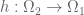 . No es para nada complicado. ¡Me encantaría contarlo la próxima vez que nos juntemos!
. No es para nada complicado. ¡Me encantaría contarlo la próxima vez que nos juntemos!
Como suponía, el teorema que quise usar antes es realmente más grande de lo necesario. Buscando con más detalle, encontré que Iss’sa, en el artículo donde prueba el teorema que menciona Pablo, prueba un `lema’ que es precisamente lo que necesitaba para hacer una prueba ‘facil’: uno simplemente encuentra un invariante que distingue los cuerpos que queremos distinguir.
La afirmación que quiero mostrar es: si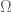 es un abierto de
es un abierto de 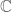 y
y  es el cuerpo de funciones meormorfas en
es el cuerpo de funciones meormorfas en 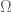 , entonces puede decidir si
, entonces puede decidir si 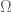 es simplemente conexo o no mirando solamente a
es simplemente conexo o no mirando solamente a  como cuerpo abstracto.
como cuerpo abstracto.
Sea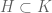 el anillo de las funciones holomorfas en
el anillo de las funciones holomorfas en 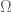 y sea
y sea 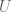 el grupo de las unidades de
el grupo de las unidades de 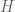 , que no son más que las funciones holomorfas en
, que no son más que las funciones holomorfas en 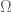 que no se anulan. Se trata de un grupo multiplicativo. Sea, por otro lado,
que no se anulan. Se trata de un grupo multiplicativo. Sea, por otro lado,  el subconjunto de las funciones de la forma
el subconjunto de las funciones de la forma  con
con 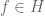 . Es un ejercicio estándar de análisis complejo mostrar que
. Es un ejercicio estándar de análisis complejo mostrar que 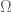 es simplemente conexo sii el grupo
es simplemente conexo sii el grupo 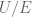 es trivial—para los que saben de que estoy hablando: uno puede mostrar que
es trivial—para los que saben de que estoy hablando: uno puede mostrar que 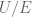 es isomorfo a
es isomorfo a  , la cohomologia singular de
, la cohomologia singular de 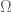 . Lo que vemos con esto es que para mostrar mi afirmación alcanza con mostrar que solamente a partir del conocimiento de cuerpo
. Lo que vemos con esto es que para mostrar mi afirmación alcanza con mostrar que solamente a partir del conocimiento de cuerpo  podemos encontrar a
podemos encontrar a 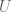 y a
y a 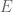 puramente de manera algebraica. Notemos que para determinar
puramente de manera algebraica. Notemos que para determinar 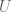 basta determinar a
basta determinar a 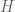 .
.
Sea el conjunto de todos los elementos no nulos. Entonces
el conjunto de todos los elementos no nulos. Entonces 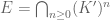 , es decir, las exponenciales son precisamente las funciones de
, es decir, las exponenciales son precisamente las funciones de  que no se anulan y que tienen raíces
que no se anulan y que tienen raíces 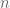 latex -ésimas para todo
latex -ésimas para todo 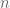 en
en  . Esto es fácil de mostrar y, a su vez, muestra que el cuerpo
. Esto es fácil de mostrar y, a su vez, muestra que el cuerpo  determina a
determina a 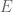 algebraicamente.
algebraicamente.
Una valuacion discreta sobre es una función
es una función 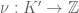 tal que
tal que  y
y  . Si
. Si  , entonces hay una valuación discreta
, entonces hay una valuación discreta  sobre
sobre  tal que
tal que  es el orden de anulación de
es el orden de anulación de 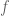 en
en  (un polo es un cero con multiplicidad negativa, a estos fines) para cada
(un polo es un cero con multiplicidad negativa, a estos fines) para cada  . Digamos que dos valuaciones discretas
. Digamos que dos valuaciones discretas  y
y  son equivalentes si existen
son equivalentes si existen 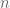 y
y  tales que
tales que 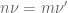 .
.
Si es una valuación sobre
es una valuación sobre  , ponemos
, ponemos  . Es fácil ver que se trata de un subanillo de
. Es fácil ver que se trata de un subanillo de  (es más: es local y su cuerpo de cocientes es precisamente
(es más: es local y su cuerpo de cocientes es precisamente  latex ; es lo que se llama un anillo de valuación discreta). Notemos que es claro que
latex ; es lo que se llama un anillo de valuación discreta). Notemos que es claro que 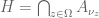 , porque una función meromorfa es holomorfa si no tienen polos.
, porque una función meromorfa es holomorfa si no tienen polos.
Ahora bien, Iss’sa prueba que toda valuación discreta de es equivalente a una valuación proveniente de un punto de
es equivalente a una valuación proveniente de un punto de 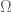 . Esto nos dice, si
. Esto nos dice, si 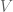 es el conjunto de todas las valuaciones discretas de
es el conjunto de todas las valuaciones discretas de  , que
, que 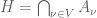 . Como el conjunto de valuaciones de un cuerpo queda determinado por el cuerpo (!), con esto probamos la afirmación que queríamos probar.
. Como el conjunto de valuaciones de un cuerpo queda determinado por el cuerpo (!), con esto probamos la afirmación que queríamos probar.
Ese lema de Iss’sa ebería poder probarse fácilmente en el caso de abiertos del plano—él lo prueba en un contexto considerablemente más general (variedades de Stein) y ahí la demostración no es complicada, … pero otra vez es un martillo para matar nuestro mosquito.
Mi final de análisis complejo fue demostrar que en un abierto conexo, toda función holomorfa se puede escribir como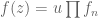 , donde los
, donde los  son los polinomios de Weierstrass amablemente modificados, y
son los polinomios de Weierstrass amablemente modificados, y  es holomorfa y nunca se anula (en complejo demostramos que si un dominio es además simplemente conexo, hay una función
es holomorfa y nunca se anula (en complejo demostramos que si un dominio es además simplemente conexo, hay una función  tal que
tal que 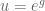 ).
).
Remmert demuestra un lema muy sencillo con caracteres de -álgebras (un caracter es simplemente un morfismo de
-álgebras (un caracter es simplemente un morfismo de  -álgebras,
-álgebras,  ). Demuestra que los únicos caracteres son las evaluaciones en un punto, y a partir de ahí es cuesta abajo ver que si se tiene un morfismo de anillos de funciones holomorfas, entonces es inducido por una función holmorfa sobre los dominios.
). Demuestra que los únicos caracteres son las evaluaciones en un punto, y a partir de ahí es cuesta abajo ver que si se tiene un morfismo de anillos de funciones holomorfas, entonces es inducido por una función holmorfa sobre los dominios.
Después el verdadero teorema de Iss’sa es ver que un morfismo de cuerpos de meromorfas manda holomorfas en holmorfas, y ahí se mete con las valuaciones… Está todo hecho sobre abiertos de y no tiene grandes complicaciones.
y no tiene grandes complicaciones.
Pablo, no depende ese argumento de que el isomorfismo de cuerpos sea un morfismo de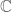 -álgebras?
-álgebras?
Volviendo al ejemplo de Carlos: sea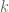 un cuerpo cualquiera,
un cuerpo cualquiera,  un conjunto infinito de variables,
un conjunto infinito de variables,  la clausura algebraica de
la clausura algebraica de  y
y 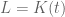 , con
, con 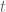 una nueva variable. Claramente
una nueva variable. Claramente  y
y 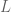 no son isomorfos, porque el primero es algebraicamente cerrado y el segundo no. Sea
no son isomorfos, porque el primero es algebraicamente cerrado y el segundo no. Sea  la inclusión. Sea
la inclusión. Sea  la clausura algebraica de
la clausura algebraica de 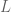 y sea
y sea  la inclusión. Si mostramos que
la inclusión. Si mostramos que  es isomorfo a
es isomorfo a  , obtenemos otro contraejemplo. Pero
, obtenemos otro contraejemplo. Pero  tiene a
tiene a  como base de trascendencia sobre
como base de trascendencia sobre 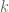 y de hecho
y de hecho  es la clausura algebraica de
es la clausura algebraica de  . Como
. Como  y
y 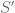 son equipotentes, hay un isomorfismo
son equipotentes, hay un isomorfismo 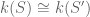 . Como la clausura algebraica es única, entonces
. Como la clausura algebraica es única, entonces 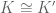 .
.
Tenés razón… el teorema de Iss’sa que tengo a mano pide que el morfismo sea de -álgebras… no sé cuán solucionable es.
-álgebras… no sé cuán solucionable es.
charlydiff no entendi bien las complicaciones que trae tu ejemplo. Pero visto inocentemente (y muy probablemente estupidamente), y suponiendo que ambos cuerpos son subcuerpos de un mismo cuerpo, un morfismo de uno a otro no implica de alguna forma que el primero es subcuerpo del segundo, y viceversa con el segundo cuerpo?
phi, en general eso es lo que uno interpreta cuando uno tiene un morfismo de un cuerpo al otro, y de hecho, se la pasa haciendo ese tipo de cosas en el curso de teoría de Galois (álgebra III) en la facultad. Por eso a primera vista muchos esperábamos que la respuesta fuera que efectivamente fueran isomorfos los cuerpos. Lo que pasa es que tener un morfismo de cuerpos te dice que tenés «una copia» del cuerpo de partida adentro del de llegada. Suena raro decir que como cuerpo, pero en realidad lo que sucede es que hay cuerpos que tienen copias isomorfas de sí mismos como subcuerpos…
como cuerpo, pero en realidad lo que sucede es que hay cuerpos que tienen copias isomorfas de sí mismos como subcuerpos…
Todavía me siento medio conflictuado al respecto, porque en un par de materias nos la pasábamos hablando de extensiones de cuerpos. Morandi dice que «K es una extensión de L [como cuerpos] si tenemos un morfismo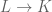 «, y define el grado de la extensión como la dimensión de
«, y define el grado de la extensión como la dimensión de  como
como 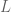 -espacio vectorial. Entonces es posible que K sea una extensión de K de grado mayor que 1. O.o. Ejemplo [copyright nico sirolli]: Sea
-espacio vectorial. Entonces es posible que K sea una extensión de K de grado mayor que 1. O.o. Ejemplo [copyright nico sirolli]: Sea 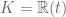 , con t trascendente, y sea
, con t trascendente, y sea  la transformación lineal «multiplicar por
la transformación lineal «multiplicar por  … entonces,
… entonces, 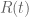 tiene una estructura de
tiene una estructura de 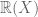 espacio vectorial (donde multiplicar por X es aplicar T). Obviamente ambos cuerpos son isomorfos, pero dependiendo de la T, la dimensión puede ser arbitrariamente grande.
espacio vectorial (donde multiplicar por X es aplicar T). Obviamente ambos cuerpos son isomorfos, pero dependiendo de la T, la dimensión puede ser arbitrariamente grande.
En esa dirección hay dos resulta dos simpáticos. El teorema de Lüroth dice que un subcuerpo de que contiene propiamente a
que contiene propiamente a 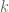 es isomorfo a
es isomorfo a  (pero, como en el ejemplo de Nicolás, no es necesariamente igual a
(pero, como en el ejemplo de Nicolás, no es necesariamente igual a  ). Un teorema de Castelnuovo, por su parte, dice que si
). Un teorema de Castelnuovo, por su parte, dice que si 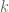 es algebraicamente cerrado,
es algebraicamente cerrado,  es puramente trascendente y
es puramente trascendente y 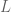 es un subcuerpo de
es un subcuerpo de 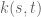 que contiene a
que contiene a 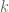 y tal que
y tal que 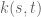 es separable y finito sobre
es separable y finito sobre 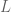 , entonces
, entonces 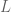 es una extensión puramente trascendente de
es una extensión puramente trascendente de 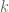 . Si la extensión
. Si la extensión  no es separable, esto es falso, y si uno mira más de dos variables, el enunciado correspondiente es muy falso.
no es separable, esto es falso, y si uno mira más de dos variables, el enunciado correspondiente es muy falso.
Estas cosas tienen significado geométrico directo. Por ejemplo, el teorema de Lüroth dice (a menos de un tecnicismo) que si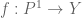 es un morfismo (de curvas algebraicas) no constante de
es un morfismo (de curvas algebraicas) no constante de  a una curva proyectiva
a una curva proyectiva  , entonces
, entonces  es tambíen
es tambíen  .
.
Hola, me parece muy interesante esta pregunta y le agradezco a Mariano por habermela mencionado. Quisiera hacer un par de comentarios, que agregan algunos contraejemplos a los ya dados, esencialmente dentro del mismo espiritu de los ejemplos del tipo de cuerpos de funciones meromorfas en abiertos del plano complejo. (sobre estos, un comentario: denotemos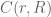 la corona de radios r y R. Entonces se sabe que
la corona de radios r y R. Entonces se sabe que 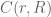 es isomorfa a
es isomorfa a  sii
sii  . No recuerdo donde vi esto ni si es facil demostrarlo. Pero pensaba que por ahi ayuda a sacar algun otro ejemplo, pero no lo veo claro).
. No recuerdo donde vi esto ni si es facil demostrarlo. Pero pensaba que por ahi ayuda a sacar algun otro ejemplo, pero no lo veo claro).
Si es una variedad algebraica irreducible sobre un cuerpo algebraicamente cerrado
es una variedad algebraica irreducible sobre un cuerpo algebraicamente cerrado 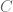 , tenemos el cuerpo
, tenemos el cuerpo 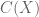 de funciones racionales en
de funciones racionales en  . (si me permiten voy directo a los comentarios, salteando por el momento las definiciones de todos los terminos standard que estoy usando). Si
. (si me permiten voy directo a los comentarios, salteando por el momento las definiciones de todos los terminos standard que estoy usando). Si 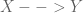 es un morfismo racional dominante entre dos variedades irreducibles entonces tenemos un morfismo (inyectivo) de cuerpos
es un morfismo racional dominante entre dos variedades irreducibles entonces tenemos un morfismo (inyectivo) de cuerpos  .
.
Existen varios ejemplos (ver mas abajo) de la siguiente situacion: variedades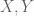 tales que
tales que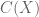 y
y  no son isomorfos (como C-algebras), o sea, como se dice, X e Y no son biracionalmente isomorfas, y
no son isomorfos (como C-algebras), o sea, como se dice, X e Y no son biracionalmente isomorfas, y
1.
2. Existen morfismos racionales dominantes
Sale de 2. que tenemos morfismos (inyectivos) de cuerpos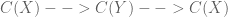
 no se supone que sea la identidad.
no se supone que sea la identidad.
y entonces un contraejemplo.
Notar que la composicion
Ejemplos:
A) espacio afin de dimension d, con lo cual
espacio afin de dimension d, con lo cual 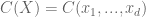 es extension trascendente pura de C, con grado de trascendencia d.
es extension trascendente pura de C, con grado de trascendencia d. .
.
Y es una cierta variedad de dimension d, provista de aplicaciones
Cualquier variedad proyectiva Y de dimension d tiene una aplicacion dominante a C^d.
Pero cuando una Y recibe una aplicacion dominante desde C^d decimos que Y es uniracional.
Entonces estamos hablando de la existencia de variedades Y que son uniracionales pero no son racionales (o sea, C(Y) no es isomorfo a C(x1, … , xd)). Y el punto es que tales Y existen. Un ejemplo es tomar Y el conjunto de ceros en C^4 de un polinomio de grado 3. Es un teorema no trivial (Clemens-Griffiths) que Y es uniracional y no-racional. Hay otros ejemplos de variedades uniracionales no-racionales. Lo que menciona Mariano en el ultimo mensaje tiene que ver con esto, ya que el teorema de Luroth equivale a decir que una variedad Y de dimension uno uniracional es racional. Pero si Y tiene dimension 3 (o mas), como en el ejemplo de Clemens-Griffiths, los dos conceptos no son equivalentes en general.
B) Tomemos ahora las dos variedades X, Y de dimension uno (curvas algebraicas proyectivas, irreducibles, no singulares). Denotemos g(X) el genero de X. Se sabe que si existe un morfismo dominante X –> Y entonces g(X) es mayor o igual a g(Y). Entonces para construir un contraejemplo estamos forzados a elegir dos curvas con igual genero. Por otro argumento, basado en la llamada formula de Hurwitz, resulta que para que haya contraejemplo debe ser
g(X) = g(Y) = 1, o sea, curvas elipticas. Y en ese caso se puede construir contraejemplo, tomando X, Y curvas elipticas isogenas (isogenous) pero no isomorfas, cosa que es posible (creo).
Esto significa que X, Y son topologicamente toros S^1 x S^1 y tenemos aplicaciones
X –> Y –> X
que son al mismo tiempo algebraicas y revestimientos topologicos, e inducen los morfismos de cuerpos deseados C(X) –> C(Y) –> C(X)
En este caso, los cuerpos C(X) y C(Y) son cuerpos de funciones meromorfas f: C –> C doblemente periodicas respecto a sendos reticulados (ver p. ej. Cartan, funcion P de Weierstrass, etc.)
Bueno, disculpen que estos ejemplos no son directos … Pero al menos muestran una vez mas que la preguntita tiene aspecto inocente pero … De todas maneras me parece que deberia ser posible encontrar otros contraejemplos elementales.
Saludos,
Fernando
Hay ejemplos interesantes de este fenómeno en http://sbseminar.wordpress.com/2007/10/30/theme-and-variations-schroeder-bernstein/.
Por otro lado, el artículo [Cater, F. S. Note on a variation of the Schröder-Bernstein problem for fields. Czechoslovak Math. J. 52(127) (2002), no. 4, 717–720. MR1940052 (2003j:12004)], que no puedo ver, parece relevante…